DeBERTaV3: Improving DeBERTa using ELECTRA-Style Pre-Training with Gradient-Disentangled Embedding Sharing

本記事はDeep Learning 論文 Advent Calendar 2022の15日目です。
本記事では以下の論文について書きたいと思います。
※ 2022/12/16 式(2)が誤っていたため更新しました。

はじめに
V1
V2
V3
おわりに

はじめに

DeBERTaV3は、2021年11月に第1版が公開されました。
Advent Calendar 2022なのに、2021年の論文を扱いますが、あまりDeBERTaについて書いている人がいなかったので、許してください、、、

DeBERTaV3は論文のタイトルの通り、2021年のICLRで発表されたDeBERTa: Decoding-enhanced BERT with Disentangled Attention(Open Review/arXiv、以下V1)のバージョン3にあたります。 V2までのモデルを継承しつつ、ELECTRAで用いられているGANライクな学習方法を、(GDESという手法で)更に改善することでV1(論文中ではDeBERTa)より下流タスクでのパフォーマンスを向上させています。そのため、本記事ではV3以前のV1, V2について最初に触れます。ここでは、BERTやRoBERTa、ELECTRAについては前提知識として割愛します。 ELECTRAについては【論文解説】ELECTRAを理解する (mm_0824氏)が参考になると思います。

※図は全てそれぞれの論文からの引用です。

V1

V1での新しい点は主に3つです。

Disentangled Attention
Enhanced Mask Decoder (EMD)
Scale Invariant Fine-Tuning (SiFT)

このうちSiFTは巨大モデルを下流のNLPタスクに適用する際に、学習の安定性を保つために使われるアルゴリズムです DeBERTaの場合、パラメータ数が1.5Bの巨大モデルをSuperGLUEに適用する際に使われており、本文中でもfuture workとして位置づけられているためここでは割愛します。

Disentangled Attention

Disentangle Attentionは、各単語 (実際はトークン) を単語 (content) embeddingと位置embedding の2つのembedding の和で表します。

disentangle
...のもつれをほどく; ...を (もつれ・混乱などから) 解き放す etc. (ジーニアス英和大辞典より)

また、各transformer層のAttentionの(単語間の)重みを、この2つをもとにしたdisentangled matrixを用いて表します。このアイデアにより、「深層」と「学習」という単語の依存性が、異なる2文の間で見られるより2つの単語が隣接していた方が依存性が強いことを表現できます。

位置 $i$ のトークンのベクトルを、内容(content)ベクトル $\{\boldsymbol{H}_{i}\}$ と位置 $j$ に対する相対位置ベクトル $\{\boldsymbol{P}_{i|j}\}$ を用いて以下のように表します。

${\displaystyle \begin{align} A_{i,j} &= \{\boldsymbol{H}_i, \boldsymbol{P}_{i|j}\} \times \{\boldsymbol{H}_j, \boldsymbol{P}_{j|i}\}^{\top} \\ &= \boldsymbol{H}_i \boldsymbol{H}_j^{\top} + \boldsymbol{H}_i \boldsymbol{P}_{j|i}^{\top} + \boldsymbol{P}_{i|j} \boldsymbol{H}_j^{\top} + \boldsymbol{P}_{i|j} \boldsymbol{P}_{j|i}^{\top} \tag{2} \end{align} }$

このように、単語間のAttentionの重みは4つの行列の和で表されます。左側から順にcontent-to-content, content-to-position, position-to-content, position-to-positionです。先行研究では前者2つは使われているものの、DeBERTaにおいては3つ目を用いており、これが重要だとしています。 4つ目のposition-to-positionについては、あまり重要な付加情報がないため実装においてはremoveされています。そのため、DeBERTaではcontent-to-content, content-to-position, position-to-contentの3つをAttentionの構成要素として用います。

これらをより詳しくAttentionの計算で見てみます。ここでは、multi-headではなくsingle-headとして考えます。ベースとなるのは一般的なself-attention (Vaswani et al., 2017)です。一般的なself-attentionは以下のように表されます。

${\displaystyle \boldsymbol{Q} = \boldsymbol{H}\boldsymbol{W}_q, \boldsymbol{K} = \boldsymbol{H}\boldsymbol{W}_k, \boldsymbol{V} = \boldsymbol{H}\boldsymbol{W}_v, \boldsymbol{A} = \frac{\boldsymbol{Q}\boldsymbol{K}^{\top}}{\sqrt{d}} \\ \boldsymbol{H}_o = \mathrm{softmax} (\boldsymbol{A})\boldsymbol{V} }$

ここで $\boldsymbol{H}$ が入力のhidden vector、 $\boldsymbol{H}_o$ がself-attentionの出力、 $\boldsymbol{W}_q, \boldsymbol{W}_k, \boldsymbol{W}_v$ がそれぞれ射影行列、 $\boldsymbol{A}$ がattention行列です。

DeBERTaではcontentを表す $\boldsymbol{H}$ の他に、相対位置を表す $\boldsymbol{P}$ を用意します。このとき、相対位置を見に行く最大値を $k$ とし、 $\boldsymbol{P} \in \mathbb{R}^{2k \times d}$ とします。 $2k$ になっているのは両側を見に行くからです。また $d$ はhidden statesの次元数で、BERTでいう768とか1024です。先程の一般的なself-attentionのように、 $\boldsymbol{H}$ と $\boldsymbol{P}$ を用いてquery, key, valueを求めます。

${\displaystyle \boldsymbol{Q}_c = \boldsymbol{H}\boldsymbol{W}_{q,c}, \boldsymbol{K}_c = \boldsymbol{H}\boldsymbol{W}_{k,c}, \boldsymbol{V}_c = \boldsymbol{H}\boldsymbol{W}_{v,c}, \\ \boldsymbol{Q}_r = \boldsymbol{P}\boldsymbol{W}_{q, r}, \boldsymbol{K}_r = \boldsymbol{P}\boldsymbol{W}_{k, r} }$

上式で、小文字のc, rはそれぞれcontent, relativeの意味です。 $\boldsymbol{V}_c$ が存在しないのは、relative positionを使ったself-attentionにおけるvalueには文意などを取るために重要な意味が含まれていないためだと推察します。

これらを用いてattention行列 $\boldsymbol{\tilde{A}}$ の要素 $\tilde{A}_{i,j}$ を求めます。

${\displaystyle \tilde{A}_{i,j} = \boldsymbol{Q}^c_i {\boldsymbol{K}^c_j}^{\top} + \boldsymbol{Q}^c_i {\boldsymbol{K}^r_{\delta(i,j)}}^{\top} + \boldsymbol{K}^c_j {\boldsymbol{Q}^r_{\delta(j,i)}}^{\top} \tag{4} }$

一気に複雑になりましたので要素を1つずつ見ていきます。まずは $\boldsymbol{Q}^c_i {\boldsymbol{K}^c_j}^{\top}$ から。これはcontent-to-contentを表す要素です。 $\boldsymbol{Q}^c_i$ は $\boldsymbol{Q}_c$ の $i$ 行目、 $\boldsymbol{K}^c_j$ は $\boldsymbol{K}_c$ の $j$ 行目を表します。

次の $\boldsymbol{Q}^c_i {\boldsymbol{K}^r_{\delta(i,j)}}^{\top}$ は、content-to-positionに対応します。ここで新しく $\delta(i,j)$ が出てきました。 $\delta(i,j) \in [0, 2k)$ はトークン $i$ からトークン $j$ への相対距離を表し、以下のように定義されます。

${\displaystyle \delta(i,j) = \left\{ \begin{array}{ll} 0 & (i-j \leq -k) \\ 2k-1 & (i-j \geq k) \\ i-j+k & (\mathrm{others.}) \end{array} \right. \tag{3} }$

$i-j \leq -k$ 、つまり $j$ が $i+k$ より後方にある場合には0が、 $i-j \geq k$ 、つまり $j$ が $i-k$ より前方にある場合には $2k-1$ が返ります。また $i$ と $j$ の距離が $k$ 以下の場合は $i-j+k$ が返ります。

$\boldsymbol{Q}^c_i {\boldsymbol{K}^r_{\delta(i,j)}}^{\top}$ の話題に戻すと、 $\boldsymbol{K}^r_{\delta(i,j)}$ は $\boldsymbol{K}_r$ の $\delta(i,j)$ 行目を表します。 $i$ に対して $j$ が

距離 $k$ より前方にあるときは $\boldsymbol{K}^r_0$ を
距離 $k$ より後方にあるときは $\boldsymbol{K}^r_{2k-1}$ を
距離 $k$ の間にあるときは $\boldsymbol{K}^r_{i-j+k}$ を

使うということですね。

最後の $\boldsymbol{K}^c_j {\boldsymbol{Q}^r_{\delta(j,i)}}^{\top}$ はposition-to-contentに対応します。 $\boldsymbol{Q}^r_{\delta(j,i)}$ は先程と同様に、 $\boldsymbol{Q}_r$ の $\delta(j,i)$ 行目を表します。

このように求めた $\boldsymbol{\tilde{A}}$ を用いて、self-attentionの出力は

${\displaystyle \boldsymbol{H}_o = \mathrm{softmax} (\frac{\boldsymbol{\tilde{A}}}{\sqrt{3d}})\boldsymbol{V}_c }$

と表します。要素が3つ分あるため、 $\frac{1}{\sqrt{3d}}$ でスケーリングすることが特に大規模なモデルの安定化のために重要とのこと。

Enhanced Mask Decoder

DeBERTaでは、エンコーダーへの入力に絶対位置を入力せず、相対位置をDisentangled Attentionで使っています。またBERTと異なり、Embeddingには位置に関連したEmbeddingを加算していません。一方で、マスクされたトークンを当てる事前学習では、絶対位置がわからないと困ることがあります。論文中の例では、"a new store opened beside the new mall"において、"store"と"mall"がマスクされ元のトークンを当てる例が挙げられています。この場合、両方のトークンは"new"と相対位置が同じ(直後にある)ため、"store"と"mall"をモデルが判別することが困難になります。

そこで、DeBERTaでは最終層の代わりにEnhanced Mask Decoder (EMD)を導入します。 Enhanced Mask Decoderはパラメータを共有した2層のTransformer Layerからなります。通常のTransformer層と同様に $\boldsymbol{K}$ と $\boldsymbol{V}$ は $\boldsymbol{H}$ から持ってきます。 2層のうち1層目の $\boldsymbol{Q}$ の入力の代わりに、 $\boldsymbol{H} + \boldsymbol{I}$ を用います。ここで $\boldsymbol{I}$ は、BERTと同じPosition Embeddingとなります。 2層目の $\boldsymbol{Q}$ の入力の代わりには、EMDの1層目からの出力を入力します。

事前学習とその結果

largeモデルは、6台のDGX-2を用い、合計96枚のNVIDIA V100を使っています。
バッチサイズ2k、1M stepsの学習で約20日とされているので、V100換算で1,920 GPU日になります。
baseモデルは4台のDGX-2 (合計64枚のV100)を使い、バッチサイズ2,048を1M steps学習させるのに10日かかっています。
換算で640 GPU日なので、ざっくりlargeサイズの1/3の計算量になります。

事前学習に使うテキストデータセットは、Wikipedia, BookCorpus, OPENWEBTEXT, STORIESを合わせて78Gになります。
RoBERTaやXLNetが160Gなので、その半分程度になります。

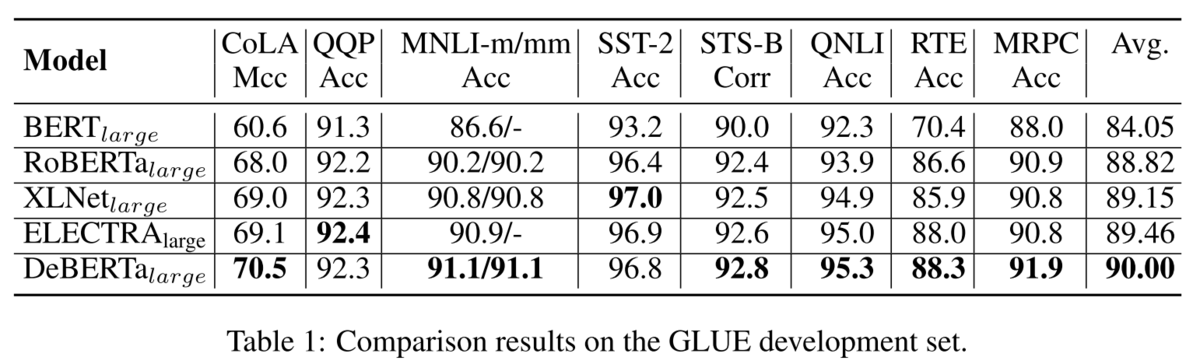
GLUEの結果は、平均的に各モデルより精度が高くなっています。

Ablationをしてみても、それぞれの要素が精度に貢献しています。

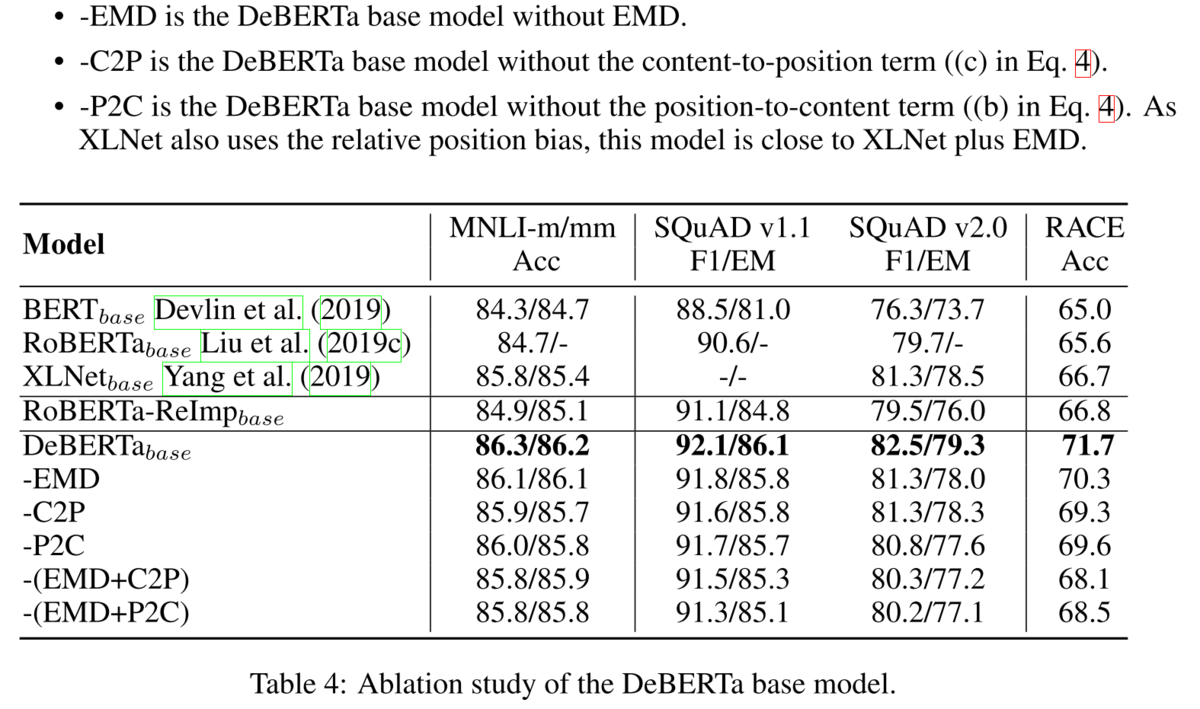
V2

V2で新しくなった点はGitHubで書かれています(論文では書かれていません)。 https://github.com/microsoft/DeBERTa#whats-new-in-v2 以下の5点が新しくなりました。

Vocabulary: GPT2 tokenizerをsentencepiece tokenizerに変更し、語彙数を50kから128kに増やしました。
nGiE(nGram Induced Input Encoding): 1層目のtransformer層の後に畳み込み層が追加されています。ablation studyについては今後追加する予定。
射影行列の共有。具体的には、V1における $\boldsymbol{W}_{q,r}$ を $\boldsymbol{W}_{q,c}$ と、 $\boldsymbol{W}_{k,r}$ を $\boldsymbol{W}_{k,c}$ と共有します。これにより、パフォーマンスに影響することなくパラメータの削減が可能に。
相対位置をエンコードする際に、T5と似たlog bucketを使用します。
サイズの大きい(900Mと1.5B)を構築したことで下流タスクでの性能を大幅に向上しました。

V3

さて、ようやくV3にたどり着きました。書いている本人もV1にだいぶ時間がかかり、本題なのにすでに息切れしております(汗)

V3では、事前学習のタスクを変更しています。従来のMasked Language Model (MLM)ではなく、MLMとReplaced Token Detection (RTD)という2つのタスクを行います。 MLMとRTDの2つのタスクを利用したモデルとしてELECTRA (arXiv/OpenReview, ICLR2020) があります。 ELECTRAを初めてお聞きの方は【論文解説】ELECTRAを理解する (mm_0824氏)が参考になると思います。 GANライクなGeneratorとDiscriminatorを持ち、GeneratorにMLMを解かせます。 Discriminatorでは、Generatorが予測したトークンが、元々のトークンから置き換わっているかの予測を行います。 MLMと異なり全トークンについて予測を行うため、計算効率を高めて事前学習を行えるというものです。また、GeneratorとDiscriminatorでEmbeddingの共有 (Embedding Sharing, ES) を行うことでも効率性を高めています。

一方で、DeBERTaV3ではELECTRAのESの非効率性を指摘しています。具体的には、Embeddingを共有することで、GeneratorとDiscriminatorの両方の学習で値を更新していくので、綱引き(tug-of-war)の状態になりやすいとのこと。実際に、Embeddingの共有を行わない(No Embedding Sharing, NES)の場合より事前学習の収束が遅いことを示しています。そこで、DeBERTaV3ではEmbeddingの共有はしつつも、Discriminatorではそれに差分を加えるGradient-Disentangled Embedding Sharing (GDES)を提案しています。 DeBERTaV1で提案されたDisentangled Attentionのように、Embeddingを共有しながらもDiscriminatorでは「2つにほどく」ようになっています。具体的には、GeneratorのEmbeddingを $\boldsymbol{E}_G$ としたときに、DiscriminatorのEmbeddingを

${\displaystyle \boldsymbol{E}_D = \mathrm{sg} (\boldsymbol{E}_G) + \boldsymbol{E}_{\Delta} \tag{6} }$

と表します。ここで、 $\mathrm{sg}(\cdot)$ は勾配の伝播をしない(stop gradient)ことを表します。つまり、Discriminatorの勾配は $\boldsymbol{E}_{\Delta}$ によってのみ更新されます。

図で比較すると以下のようになります(左から順にES、NES、GDES)。

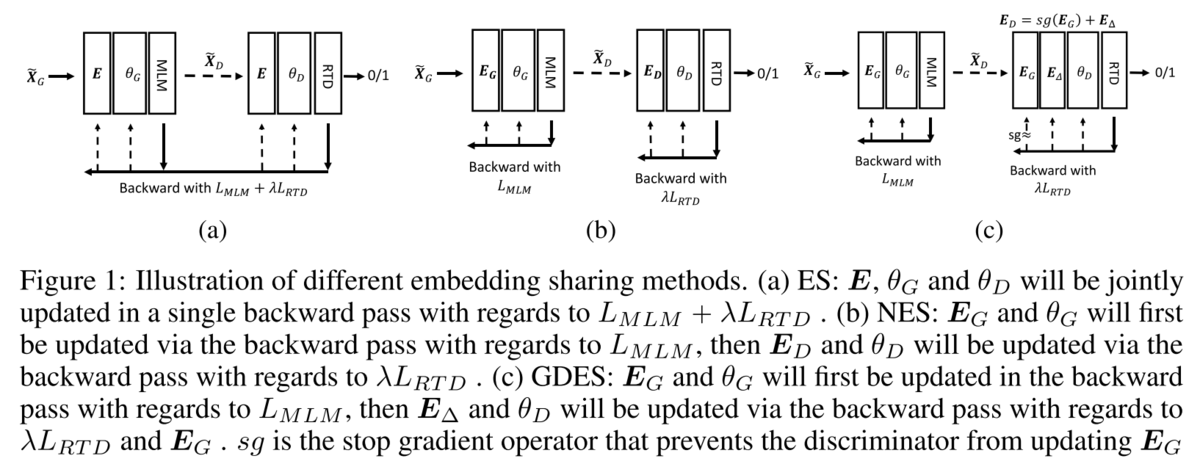
GDESの学習の順序としては、まずGeneratorのMLMのforwardとbackwardを行い、 $\boldsymbol{E}_G$ を更新します。次に、Generatorで作成された入力をもとにDiscriminatorのRTDのforwardとbackwardを行います。 backwardでは $\boldsymbol{E}_{\Delta}$ のみが更新され、更新された後に $\boldsymbol{E}_G$ に加えられDiscriminatorの次のEmbedding $\boldsymbol{E}_D$ を構成します。 $\boldsymbol{E}_{\Delta}$ の初期値は0行列となります。

3つのEmbedding共有の手法の下流タスクでの性能を比較すると、GDESが最も性能が高いことがわかります。

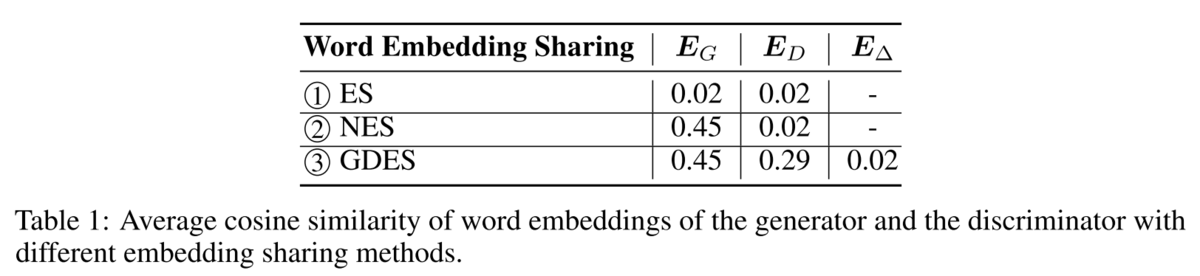
このGDESを用いてDeBERTaV3 largeを構築します。 ELECTRAと異なり、DeBERTaV3ではGeneratorがDiscriminatorの半分のtransformer層の数になる以外は全て同じモデル構造となります。 (ELECTRAではGeneratorがDiscriminatorの1/3～1/2のサイズになっています) こうして構築したDeBERTaV3は、DeBERTaV1を含む他のモデルに比べて更に高い性能を持っていることを示します。

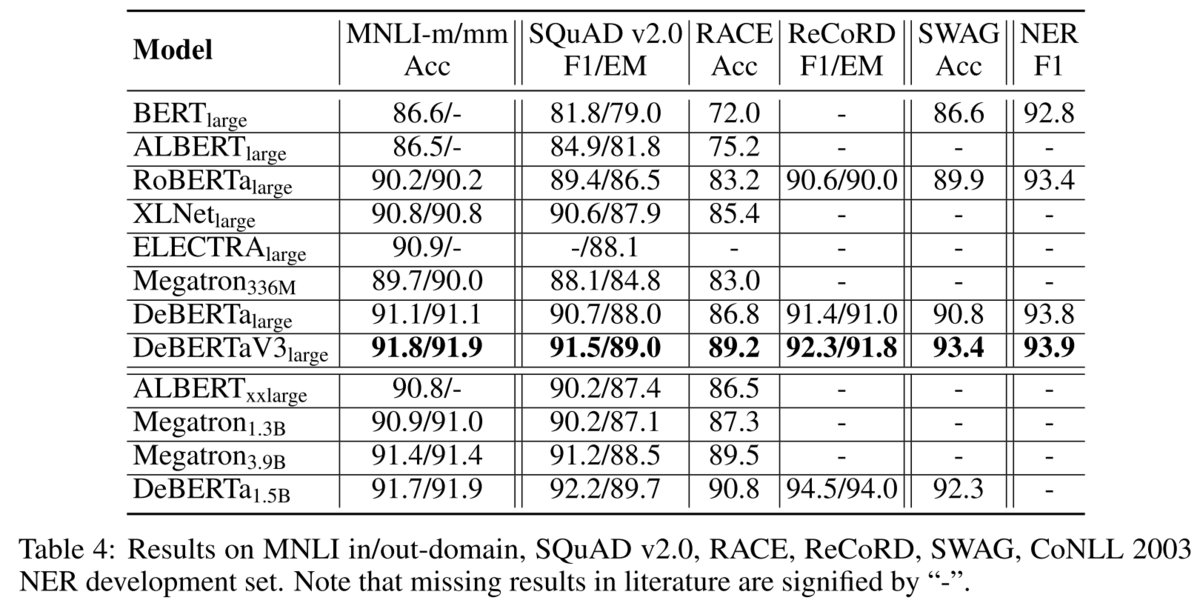
smallモデル(ELECTRAのsmallとは異なるサイズ)でも他のモデルと比べて高い結果を示すことが論文中のTable 5で示されています。

おわりに

DeBERTaV3の記事の予定が、DeBERTaV1が大部分となってしまいました。 DeBERTaV1, V2, V3ともにHuggingFaceでモデルが公開されているので、簡単に利用できるようになっています。詳細なまとめはフリーで使える日本語の主な大規模言語モデルまとめ (HelloRusk氏)に譲りますが、日本語ドメインでは

がメジャーどころでしょうか。 (最後のELECTRAは私が構築したものです) 日本語ドメインで論文を書くときには最新のメジャーモデルで実験を行うことが求められがちなので、DeBERTaでも日本語モデルが公開されることを期待しております。 (私も作ってみようかしら、、、)

retarfiの日記

自然言語処理などの研究やゴルフ、音楽など。